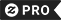Wiskunde wandklok (medium) ronde klok

Als je de voorkeur geeft aan interessante wiskundige theorieën en concepten boven zinloze nummergekrompen (zoals je kunt zien in de meeste andere design), dan kan dit het juiste product voor je zijn. Als een van de punten onduidelijk is, raadpleegt u de onderstaande lijst voor een korte uitleg en beschouwt u deze als een uitgangspunt voor verder onderzoek. 0 [sic!] - Algemene wiskunde: Door een verbazingwekkende identiteit van Leonhard Euler is deze expressie gelijk aan 0. Het wordt door velen beschouwd als een van de mooiste vergelijkingen in de wiskunde. 1 - Axiomatic Set Theory: de set die alleen de lege set bevat. Zo wordt 1 gedefinieerd in von Neumann's bouw van de koralen. 2 - Lineaire algebra: De dimensie van de reeks complexe aantallen, wanneer gezien als echte vectorruimte, is gelijk aan 2. De meest natuurlijke basis bestaat uit de twee elementen 1 en i. 3 - de Theorie van de Grafiek: Het chromatische aantal van de grafiek van Petersen is gelijk aan 3, zo betekent het dat zijn toppen met drie kleuren kunnen worden gekleurd zodat geen twee aangrenzende toppen de zelfde kleur krijgen. Overigens is de grafiek van Petersen beroemd om zijn beruchte tegenhanger van veel optimistische voorspellingen over grafieken. 4 - Combinatoriek: de exponentiële groei van de Catalaanse aantallen is gelijk aan 4. Deze getallen zijn opmerkelijk omdat ze voorkomen als de tellende opeenvolging van letterlijk honderden verschillende combinatoriale structuren. 5 - Geometrie: er zijn precies 5 platonische vaste stoffen, dat wil zeggen regelmatige en convexe polyhedra. Zij worden genoemd naar het aantal gezichten: tetraëder (4), hexaëder (6), octahedron (8), dodecahedron (12) en icosahedron (20). 6 - Nummertheorie: voor elk natuurlijk getal n vertelt de totientfunctie van Euler ons hoeveel getallen er in 1 zijn...,n die relatief priemgetal zijn . Aangezien n = 7 zelf een priemgetal is, zijn er 6 van dergelijke getallen, namelijk 1,2,3,4,5,6. Om het even welk efficiënt algoritme voor gegevensverwerking deze functie zou onmiddellijk het wijd gebruikte de encryptieschema van RSA breken. 7 - Probability Theory: In verwachting, resulteert het rollen van twee gebruikelijke dobbelstenen in 7. Overigens heeft de wiskundige kansrekening zijn wortels in het begrijpen van kansspelen, zoals het rollen van dobbelstenen en het omdraaien van munten. 8 - Codingtheorie: nummer 8 heeft de representatie 1100 in binaire grijze code. Vergeleken met conventionele binaire coderingen, hebben de Grijze codes het soms wenselijke bezit dat het coderen van twee opeenvolgende aantallen in precies één beetje verschillen. 9 - Real Analysis: Dit is een convergerende oneindige reeks. De grenswaarde ervan wordt geacht gelijk te zijn aan 9 door gebruik te maken van de formule voor oneindige geometrische reeksen. 10 - Complexe analyse: Met de coëfficiënt van Cauchy kunnen coëfficiënten worden geëxtraheerd uit de Taylor-expansie van een analytische functie. Merk op dat (1+z)^5 de genererende functie voor de binomiale coëfficiënten (5 kiezen 0) is, (5 kiezen 1), ..., (5 kiezen 5). 11 - Formele talen: Het afgebeelde koord behoort tot de regelmatige taal van hexadecimale aantalliterals. De semantische waarde van dit koord is 11.