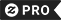Pythagorean Theorem Proof met soortgelijke driehoe Extra Grote Mok

Bewijs met soortgelijke driehoeken Dit bewijs is gebaseerd op de evenredigheid van de zijkanten van twee vergelijkbare driehoeken, dat wil zeggen op het feit dat de verhouding van twee overeenkomstige zijden van soortgelijke driehoeken gelijk is ongeacht de grootte van de driehoeken. Laat ABC een juiste driehoek vertegenwoordigen, met de juiste hoek die bij C wordt gevestigd, zoals aangetoond op het cijfer. We tekenen de hoogte van punt C en noemen H de snijpunt met de zijkant AB. Punt H verdeelt de lengte van de hypotenusa c in de delen d en e. De nieuwe driehoek ACH is gelijkaardig aan driehoek ABC, omdat zij allebei een juiste hoek (door definitie van de hoogte) hebben, en zij delen de hoek bij A, betekenend dat de derde hoek ook in beide driehoeken het zelfde zal zijn, duidelijk zoals in het cijfer. Een soortgelijke redenering is dat de driehoek CBH ook vergelijkbaar is met ABC. Het bewijs van gelijkenis van de driehoeken vereist het postulaat van de driehoek: de som van de hoeken in een driehoek is twee rechte hoeken en komt overeen met het parallelle postulaat. http://en.wikipedia.org/wiki/File:Pythagoras_similar_triangles.svg